Upon completion of lecture on Egyptian Multiplication, these ninth grade general mathematics students will be able to multiply any two numbers using the egyptian algorithm with ninety-five percent accuracy.

Objectives:

Upon completion of lecture on Egyptian Multiplication, these ninth grade general mathematics students will be able to multiply any two numbers using the egyptian algorithm with ninety-five percent accuracy.

These students will need to satisfy the following before they will be able to complete the main objective.

• Multiply by two or add a number to itself.
• Set up the basic outline for the algorithm.
• Add larger numbers together to get an answer.

Plan:

This lesson plan will be about a new type of algorithm that will help those of you with problems multiplying numbers. This algorithm is entitled Egyptian Multiplication. This method was used and developed by the ancient Egyptians. These were people who migrated from the fertile Sahara region of Africa. The Egyptians had customs similar to those of the Ethiopians. The Egyptian civilization was one of the greatest ancient civilizations. They were well organized and one of the more advanced of the ancient civilizations. They had calendars, standard weight and measure system and a centralized government.

Egyptians used a different way to write the numbers than we do. Their writing is called hieroglyphics. This type used different pictures to stand for different numbers. The list that follows is what these hieroglyphics look like:

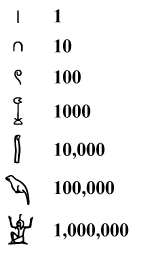
Egyptians had an interesting way of doing multiplication. They used addition to get the answer of a multiplication problem. They only had to memorize one multiplication table. That table would be the 2 times table. This method is still used in many rural communities in Ethiopia, Russia, the Arab World, and the Near East.

The term that we use with Egyptian Multiplication is called Doubling. Doubling does just what it sounds like. You take one number and either multiply it by 2 or you add it to itself. This is done repeatedly until you get the other number. Below is an example of what you need to do using the problem 22 x 21:

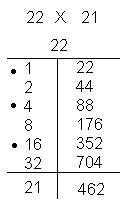
You first take either number, the 21 or 22. Here we used the 22. Then set up a little chart like we have done. Put the number being doubled on the right hand side. On the left hand side you put the "double number". You keep putting the orresponding double with the number that was doubled. Once you get to a double larger than the other number you are multiplying then you can stop. Now you have to find the double numbers that add up to the other number, in our case is 21. The doubles that add up to 21 are 1, 4, and 16. Take the corresponding numbers and add them together; 22+88+352=462. That number is the product of 22 and 21. Below are some more examples:

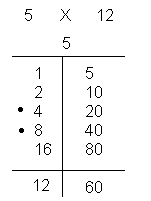
After completing these examples with the help of the class. I would then ask them for some number that they would like to see multiplied together using this method. We would do these together with the class telling me the doubles of the number. After about 10-15 minutes of this activity, I would then ask them for five more pairs of numbers that they want multiplied. Once I write the numbers on the board, I would tell them to copy these own and do them for homework that would be collected tomorrow in class and is worth the same amount as a quiz. Before our departure, I ask them if they have any questions. If so, I would answer them. I also remind them if they need extra help I would stay after school for about 2 hours.

Comments: